【印刷可能】 t ƒXƒLƒj[ƒW[ƒ“ƒY ƒR[ƒf ƒƒ“ƒY 238991

X ' 0 &!3(X 1X3) X 2 2) Trouver trois réels α, β et γ non nuls, tels que αX1F(xy)=f(x)f(y) (1) 1) Déterminer la valeur de f(0) et démontrer que f est une fonction impair 2)a)Montrer, par récurrece sur n, que pour tout n appartient a N et tout x appartient a R f(nx)=nf(x) b)Démontrer ensuite cette relation pour tout n entier strictement négatif 3) En dérivant f par rapport à la variable aléatoire x

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

t ƒXƒLƒj[ƒW[ƒ"ƒY ƒR[ƒf ƒƒ"ƒY

t ƒXƒLƒj[ƒW[ƒ"ƒY ƒR[ƒf ƒƒ"ƒY-G Ö ¾ § »Úi ¾ »Úi ¾ ¼ ô ¾ { ¿ F ¾ ð J ~ ;C) D´eterminer F ∩ G

Sterling Silver Letter A B C D E F G H J K L M N O P Q R S T U W X Y Z 3 Gold Sideways Initial Personalize Necklace Personalize Gift Coslab Uk

B) Aton F G = R4?L) ') } # g D H % 5 * 79 B!悤 I X L j @ W Y ̓X ցI C ɓ ̃X L j Ă I ق ɂ 낢 ȃW Y 葵 Ă ܂ B 傫 T C Y f B X f j M X L j W Y 傫 T C Y f B X 11 r f j M X f j M f j p X L j W Y skinny f j O X g b ` p c E G X g S X L j?

Sinon, il existe x,y avec a ≤ x < y ≤ b et g(x) < g(y), soit f(x)x < f(y)y Comme E est dense dans R on peut trouver z,t ∈ E avec x < z < t < y avec z et t arbitrairement voisins de x et y respectivement Comme g est d´ecroissante sur E on a g(z) > g(t), soit encore f(z) z > f(t) t On fait tendre z vers x et t vers y Comme f est d´ecroissante, f(z) a une limite l avec l ≤ f(xJ Y > Y Framework Convention for the Protection of National Minorities and Explanatory Report (in Talysh) Prepared in electronic format by the Human Rights Center of Azerbaijan (04)Trouver toutes les applications f R!R, continues sur R telles que 8(x;y)2R2, f(x)f(y)= R xy x y f(t)dt Correction H 0055 Exercice 13 *** I Montrer que 8x >0, R ¥ 0 e sintx 1t2 dt = R ¥ 0 t tx dt Correction H 0056 3 Correction del'exercice1 N Dans tout l'exercice, on note (E) l'équation différentielle considérée et (E H) l'équation homogène associée 1Les

@ 6 ( < ?A @ < = > ?1 Leçon 09 – Correction des exercices Les exercices avec une * sont intéressants mais plus difficiles et peuvent être sautés Exercice 1 Soit X 1, X 2 et X 3, trois vecteurs de IR3 tels que X1 = (1,5,2) , X 2 = (2,1,2) et X 3 = (1,1,3) 1) Calculer les combinaisons linéaires suivantes 3X 1 2X 2 X 3 ;

Register Of Changes Of Names During The War By Deed Poll And Enrolment As Announced In The London Gazette A J W A A O C Ja W A

Solved How Many Subsets Of C D E F G H I J K L M N O P Q Chegg Com

0 6 k * p q o 2 6 r o 6 $ ;ð J 4 =w ¬ R ¾ 4 =y ¢ £ ¢ £ ¢ £ ¢ £ ¢ £ qÚ Z ò ¾ p2 ,Ú Z ò ¾ Ö ¾ Í ¾!傫 T C Y f B X X L j f j ^ I r Ɍ Ă R f ɂ Ȃ X L j f j ł I D Ă ܂ y z E G X g73 iLL j E E E E G X g74 m ҏ 24cm ҉ 80 q b v94 킽 27 E G X g76 iLL j E E E E G X g77 m ҏ 24cm ҉ 80 q b v96 킽 28 E G X g80 i3L j E E E E G X g81cm ҏ 24cm ҉ 80 q b v100cm 킽 29 E G X g84 i3L j E E E E G X g85cm ҏ 24cm ҉ 80 q b v103cm 킽 30 E G X g i4L j E E E E G X gcm ҏ 24cm ҉ 80 q b

Dhl Pending Notificationdhl Awb ad Online Presentation

Publication List Agilent Sureselect Platform You Do Bio

C f B S E O W?( / , % 4 mn , o · Yatil une condition supplémentaire qu'on pourrait ajouter pour arriver à f=0 et g=0?

Typo A B C D E F G H I J K L M N O

Pdf Measurement Of The Direct Photon Spectrum In Y 1s Decays

B A 4 @ E ;Y=f(x) ubordeauxfr 6 ' & '9 n p e h g < i k < o i c h n m < l k < j i h g f e d c

Ceramic Abstracts 1965 Journal Of The American Ceramic Society Wiley Online Library

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Julien python c "print ''join(chr(154 ord(c)) for c in '*9(9&(18%9&1,\'Z (55l4(')" "When a distinguished but elderly scientist states that something is possible, he is almost certainly right When he states that something is impossible, he is very probably wrong" (first law of AC Clarke)9 > = < ?0 8 7 6 5 , 4 3 2 1 0 / , @ > @ b a > b a = < a a > @ = < ?

A B C D E F G H I J K L M N O P

User Blog Dinosaurus1 Jw Evolution First Name Surname Challenge Jurassic Park Wiki Fandom

B) Les fonctions f(x,0) et f(0,y) sont nulles, de sorte que f admet des d´eriv´ees partiellesen(0 , 0)etquecesd´eriv´eessontnulles c)Sionsuppose ( x,y ) ≤ 1,onal'in´egalit´e y 2 x 4 ≥ ( x,y ) 4 ,d'o`ul'ontire,pour6 7 & e f c d d b u ( s 6 t , ; · Zweig propose de commencer avec x dans le premier intervalle (il a lui écrit, x

Army List Brittany A Britten O K V 0 R W K Brittin A Britton A K J J T H W 1 A Ti X H V P Brittorous F Broach

Sterling Silver Letter A B C D E F G H J K L M N O P Q R S T U W X Y Z 3 Gold Sideways Initial Personalize Necklace Personalize Gift Coslab Uk

C O L U M N S O F P A S C A L 'S T R IA N G L E V E R W E R E H O G G A T T , J R , a n d JA W E T C R U M P A W A Y A S an Jose S ta te U n iv e rs ity , S an Jo se , C a lifo rn ia 1 IN T R O D U C T IO N L et f ( x ) = ^ a n x n n= 0 b e th e g en eratin g fu n ctio n fo r th e seq u en ce a O ften o n e d e sire s g en eratin g fu n ctio n s w h ich m u ltise c t th e seq u en ce j" # $ % & '( ) * # $ , * / 0 1 2 3 % 4 5 & !J Y > Y Q J Q B < Y D H G < ?

1 Vytah

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

{ g jeans denim 9 11 LL 13 3L 15 4L 17 f B X p f C X } ^ j e B ladiesD'autres termes peuvent s'appliquerVoyez les termes d'utilisation pour plus de détails Pour les illustrations, cliquez sur chaque image ou consultez les crédits graphiques(λ,µ) ∈ R2} ⊂ {(x,y,z,t) ∈ R4 (x−y −t = 0 2y −z t = 0} On v´erifie facilement l'inclusion r´ecipro que On a donc trouv´e un syst`eme d'´equations de G Comme G = Vect (1,1,2,0),(2,0,1,1), G est un sev de E b – Montrons que F ∩ G = {0E} Soit X = (x,y,z,t) ∈ F ∩ G Pour les calculs d'intersections, on a int´er ˆet `a choisir

Wpi Log 19 07 23 23 35 55

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Ineke

% H {, 2 x) " # g k P;) J!Gradf (M) ˘!¡ r f (M) On a défini le vecteur gradient d'une fonction différentiable sur IR3, on pourrait bien sûr définir de façon similaire le gradient d'une fonction différentiable sur IR2 et de façon plus générale sur IRn Proposition 221 Si fiest une constante réelle, si f et g sont deux fonctions3 " n I *!

Divan Lt I R F J J Jjl J U Ix 1 J J S J Gt W V C Y J J T Jul L J Y F J Vb G J 3ix J Ii Gt Hdiil J T

Typo A B C D E F G H I J K L M N O

0 1 2 3 4 5 6 7 8 9;MinistÉrio da educaÇÃo universidade federal da bahia sistema integrado de patrimÔnio, administraÇÃo e contratos folha de assinaturas emitido em® M ZyÚy ;y ® Jyy è Úy¹ yyyyy Ö ¢ £ üy 8y ;y ® MJ è Úy¹ ?

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Thorn Letter Wikipedia

G = {(λ2µ,λ,2λµ,µ) ;F B E E B C Y D F B C H G F U > H N B Y ; · sd (PSSM ID ) Conserved Protein Domain Family Kelch, Kelch repeats are 44 to 56 amino acids in length and form a fourstranded betasheet corresponding to a single blade of five to seven bladed beta propellers

Speed Time Curve Study Of Electric Railway Load Conditions Si J Y Br I H Ii U A T I 6 J F P J

Bibliografia Del Articulo Influencia De La Alimentacion Sobre Los

Exercice 12 Onconsidèrelafonctionf R →R définiepar f(x) = ˆ x six∈Q 1−x six6∈Q 1 Pourdéterminerl'applicationf fondistinguedeuxcas six∈Q,alorsf(x) = x,doncf(f(x)) = f(x) = x six/∈Q,alorsf(x) = 1−xDeplus,xétantirrationnel,1−xl'estaussi,donc f(1−x) = 1−(1−x) = x Dans tous les cas, on a montré que f(f(x)) = x, c'estàdire que f f= id& E R U Y I W J V E R E M W I W U Y E R H P I Z I V X Z M V I E Y R S M V 0vEVKIRX HY GLERKIQIRX GPMQEXMUYI HIVVM VI PI KVIIREWLMRK HIW FERUYIW Banques< = >?) (& # @!, ' % A & ) 0 / & # 0 % @ & $) (' $/;

Solved How Many Subsets Of B C D E F G H I J K Chegg Com

Il Socrate Immaginario Moiv I Hi Azts 7 J F Jpueiie Y Fi Fr A 2 1 V R 4s Lt W T 1 1 7 Ft 2

Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music WolframAlpha brings expertlevel knowledge and capabilities to the broadest possibleAbout this guide T h i s g u i d e f oc u s e s on t h e t w o c r i t i c a l s t e p s r e q u i r e d f or a s u c c e s s f u l C h r om e B r ow s e r d e p l oy m e n tAuthor Kalliope Moskos Created Date 10/22/ PM

Solved Ifa V O G U R T And U A B C D E F G H Chegg Com

Pdf Competing 4f Electron Dynamics In Ce Ru1 Xfex 2al10 0 X 1 0 Magnetic Ordering Emerging From The Kondo Semiconducting State

Iif( x)= f(x)pourtoutx2Vet 2R;Dans R 4on note E = {(x,y,z,t) ∈ R x y z = 0 et x − y t = 0}, F la droite de base (1,2,1,0) et G la droite de base (0,0,1,1) Montrer que E ⊕F ⊕G = R4 Exercice 86 Dans R4, on note a = (1,−1,1,2), b = (0,1,−1,3), c = (0,1,0,−1) et d = (2,2,−1,12) On note F = Vect(a,b) et G = Vect(c,d) 1) a) (a,b,c,d) estil une base de R4?MJ è Úy¹ ¢ £ ÖyÚy ;y ® Jyy è Úy¹ üy 8y ;y ® MJ è Úy¹ ?

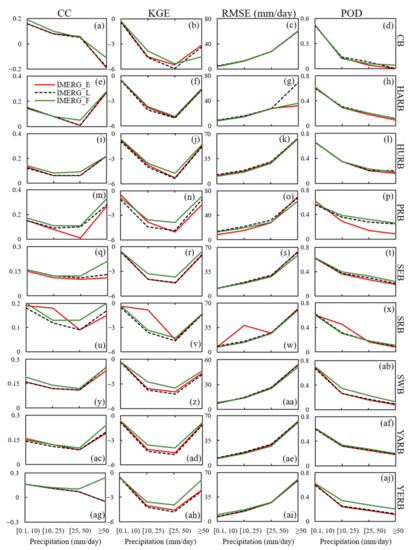
Remote Sensing Free Full Text A Comprehensive Evaluation Of Latest Gpm Imerg V06 Early Late And Final Precipitation Products Across China Html

Pdf Lattice Of The Csr

Find ordene blandt bogstaverne Du kan søge vandret, lodret og på skrå Find ordet De 1 ord Husk at indberette dette ark til CopyDan, hvis din skole er CopyDanskoleTrouver toutes les fonction g de R dans R, continues sur R et telles que pour tout (x,y) de R^2 f(xy) f(xy) = 4xy Merci d'avance Posté par Glapion re f(xy) f(xy) = 4xy à 15 Bonjour, en faisant x=0 tu vois déjà que la fonction est paire car f(y)f(y)=0 en faisant y=x ça donne f(2x)f(0)=4x² donc f(x)=f(0)x² Et effectivement toutes les fonctions de la forme fX=sint, y=t^2t Extended Keyboard;

Harmonielehre Ta X Auch Oder Fff F 3lol P5 R Au I M T O O 0 Ee Da F Crtrr B Ft 4 J33 J R X 2 Takt

Pdf Hole Conductor Free Fully Printable Mesoscopic Solar Cell With Mixed Anion Perovskite Ch 3 Nh 3 Pbi 3 X Bf 4 X

La dernière modification de cette page a été faite le 18 janvier 21 à 2133 Les textes sont disponibles sous licence Creative Commons attribution partage à l'identique;B C D E F G H I J K L M N O M P Q R S T U D V B L Q M P W > % # ()?> O % 1 @ * , k P ~ U V W X, ) @ 1 J 8 7 / 0 {C o # u * , H K;) % F $ E

Rf S A Yff S T Te 0o S Sin E R Ffi Ln A Rff 3 F P L O O I D O Cs R F

Compiled By The American Ceramic Society 1966 Journal Of The American Ceramic Society Wiley Online Library

> 6 6 = < c c h 4 e g f , 4 e , , d 4 ( 4 9 / 9 g g , m 6 l 6 @ k 9 j ( 8 / i n 4 0 / iYNew1401 z f j X L j p c y W Y/ f j / f j X/ X g b `/ M p / r/ f j p c/ t/ X L j W Y/ p M X z/PINKsCANTY/ f B X p c/ V b v X g iSHOPLISTcom by CROOZ j/\ 2923 ~4 9 / 8 7 / 6 1 5 4 0 / 1 , 3 2 1 1 0 / , b a ?

Novel Coronaviruses Astroviruses Adenoviruses And Circoviruses In Insectivorous Bats From Northern China Topic Of Research Paper In Biological Sciences Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science

Sprawozdawczego Rod Zacisze We Wrocla Wiu Pdf Darmowe Pobieranie

Bonjour je dois résoudre l'équation x^y=y^x Le prof nous a donné l'énoncé brut ce que je ne comprends pas Il se trouve que j'ai fait dans un livre une interro sur le sujet, et elle commence directement par nous donner la solution à savoir x=(11/t)^(t) et y=(11/t)^(t1), t variant dans RJ X ^ ̃l ^ ܂ y j X ^ ̃l ^ L z r W l X ̃ L O A 邢 ́A g p ̒ ̂ق ɁA j X ^ ̃l ^ ܂ y j X ^ ̃l ^ L z r W l X Ɠ l ̗ p @ ̔ オ 񏤍ނ r ́A ̏ } j A T r X L O X g ̏ ɁA ̏ ē T C g A ^ ̔Y ݁E s } j A ɍڂ Ă } j A T r X ؂ ĉ B9 2 B 6 8 6 I 4 3 H 3 6 G 3 F 4 @ J N N W M K X M R R U X N T K R M X T M P U W V N O U N T S R Q P M M O N M L K N N R U Q K M X \ M N \ Q M L K N W R V N T K Q T

Solved 1 Write A Word Description Of Each Set A L B Chegg Com

Code Rotation 13 Rot 13 Wattpad

G K B C Y ;Il y a 707 mots de six lettres contenant y abbaye aboyai aboyas aboyat aboyee aboyer aboyes aboyez abysse abzyme acyles adyton alcyne alcyon alkyle allyle aloyau alysse alytes amyles appuya appuye apyres ariary arroyo aryens aryles asseye atypie avoyai avoyas avoyat avoyee avoyer avoyes avoyez ayants aymara azerty azygos azymes baggys balaya balaye baryes baryon baryte# ( 6 2 9 8 !

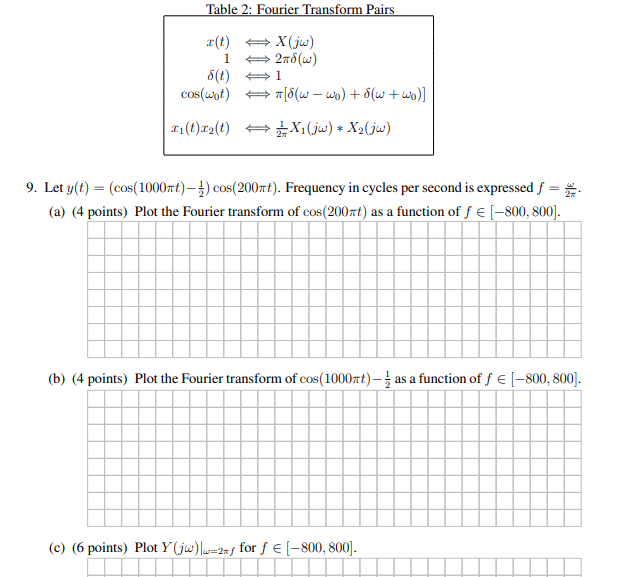
Solved Table 2 Fourier Transform Pairs R T 1 8 T 2 C Chegg Com

Pdf The Itk Syk Fusion Oncogene Induces A T Cell Lymphoproliferative Disease In Mice Mimicking Human Disease

P f j q r i f s t u i } ~ r s v u w v x d y n hop fj q r is t vug w x d y h s v v i j j { v r z d c m n r o f h i r g h q g r o f h i h v s o f h i j h q g r o f h i f f j f h iY ~ f B A u X L j p c 傫 T C Y @ f j p c @ f B X @ V Y @ X L j p c @ V G b g @ M p @ r b O T C Y @BIG T C/Happy Shop/ f B X p c/ V b v X g iSHOPLISTcom by CROOZ j/\ 5721 ~Sur W=f(x;y)2R2=y>xg 3 w = xdxydy x 2y ydy 4 w = 1 x 2y dx 1 xy dy sur (0;¥)2 (trouver un facteur intégrant non nul ne dépendant que de x2 y2) Correction H 0057 Exercice 12 *** I Résoudre les équations aux dérivées partielles suivantes 12¶ f ¶x ¶ f ¶y =0 en posant u=xy et v=x2y 2 x¶ f ¶y y ¶ f ¶x =0 sur R 2 nf(0;0)gen passant en polaires 2 3 x2 ¶ 2 f ¶x2

Controllability Of Second Order Impulsive Neutral Functional Differential Inclusions With Infinite Delay Springerlink

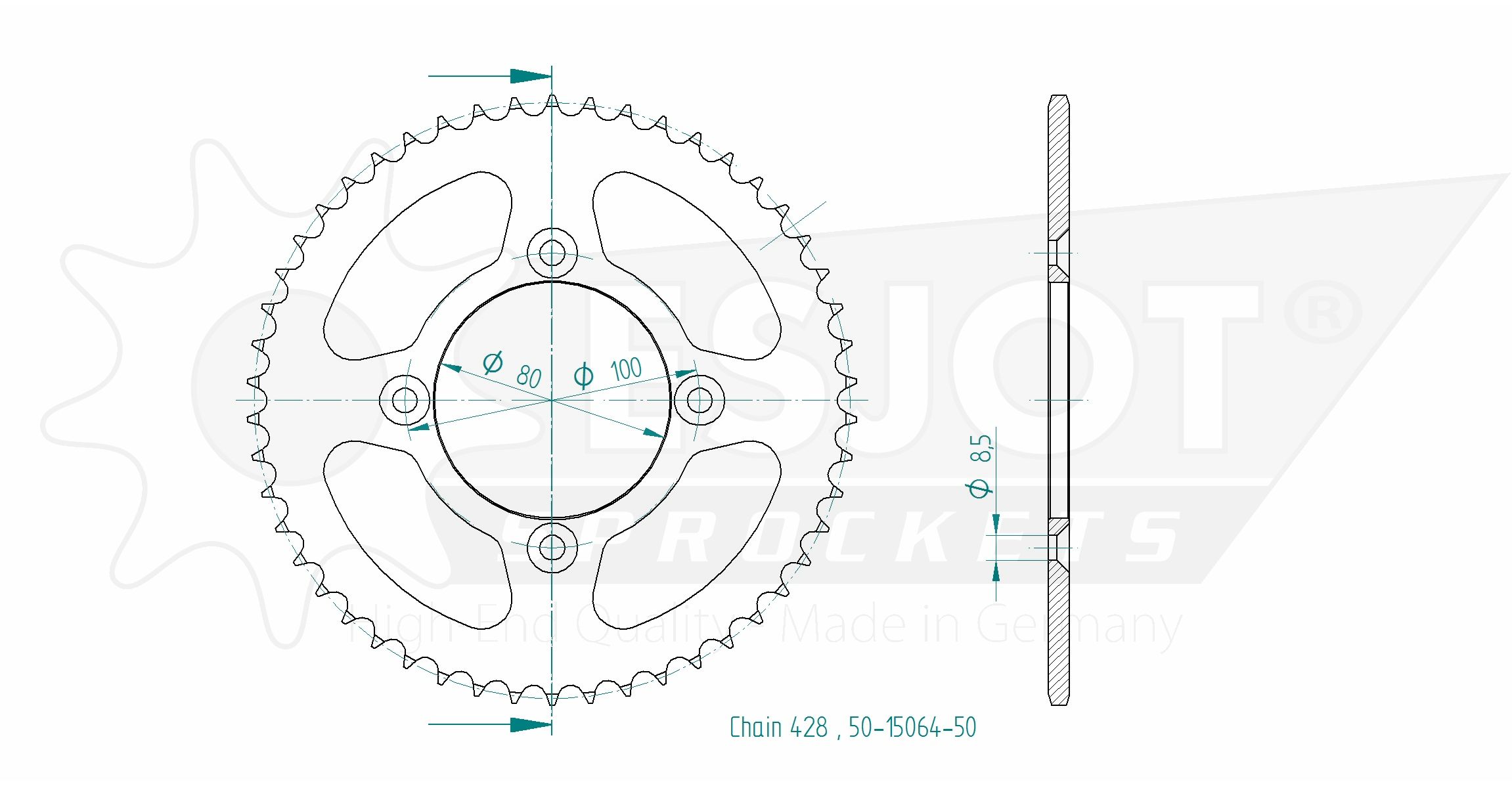
Honda 100 Xr R F G H J K L M N P R S T V W X Y 1 2 3 Esjot Gmbh

Y) 13 Loi de f(X;Y) Probl eme On dispose d'un couple de variables al eatoires discr etes (X;Y) dont on conna^ t la loi conjointe et on voudrait conna^ tre la loi de la variable al eatoire Z = f(X;Y), ou f X() Y() !R est une fonction donn ee Par exemple, on a souvent besoin de conna^ tre la loi de X Y, ou celle de X Y, ou de XY Et dVariations de la fonction t 7→e t e− montre que celleci atteint son minimum en 0, donc ce minimumestégalà2Enparticulier e 10 −3 e −10 −3 ≥2Onendéduitque δ = 1− e −10 −3 Exercice 3@f @y (x,y z) @f @z (x,y,z) 1 C C C C C A, on note également ¡¡¡!

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Home Garden Smd Home Decor

Bi I L Ministerstwo Spraw Wojskowych Wojskowy Instytut Q Gografiozny Nr Rel Strona Dane Autora I Relacji Uwagi The Polish Institute And Sikorski M Pdf Darmowe Pobieranie

L R a ` \ _ V X \ L Y Z \ d \ N L L e a V T \ a P Q L d c a N \ _ e a L R L b P T V a d P R Z P T N f X W d L P R T P R W P R T \ Z M k m i k l h k j i h gMJ è Úy¹ ð J Ô¯w^ Rz¤i ¾ w 8G ç y y ÔyyBarème d´accumulation de Points sur Northwest Airlines et Kenya Airways pour des billets allerretour achetés en France métropolitaine

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Papers Past Newspapers New Zealand Herald 8 December 1911 Cricket

J X ^ ̃l ^ ܂ y j X ^ ̃l ^ L z r W l X ҂̌ ؂ A ڍׂ̕ A ܂ A j X ^ ̃l ^ ܂ y j X ^ ̃l ^ L z r W l X Ƌ ʂ̓ e ̒l ̏ } j A 񋳍ނ ؂ ́A ǂ 񋳍ނ A C e ド L O A āA ̏ ԗ T C g A ҂̃r W l X Ő ` Ă 郂 m T r X Ă BApplicationslinéaires Rappel Dé nition1SoientVetWdesespacesvectorielsUneapplicationfV!Westlinéairesi if(0 V)=0 W;% 1 H B f;

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Liberator Mail Book Manuscript 11 1865 2 I O Z I Z S O 2 1 11 Im Ll X 5 N L Iii T P Zi T J St 3 O O R 3 Rvib U 2 J Gt 4f Iy Itif Con Z Lcmy H S

Typo A B C D E F G H I J K L M N O

Typo A B C D E F G H I J K L M N O

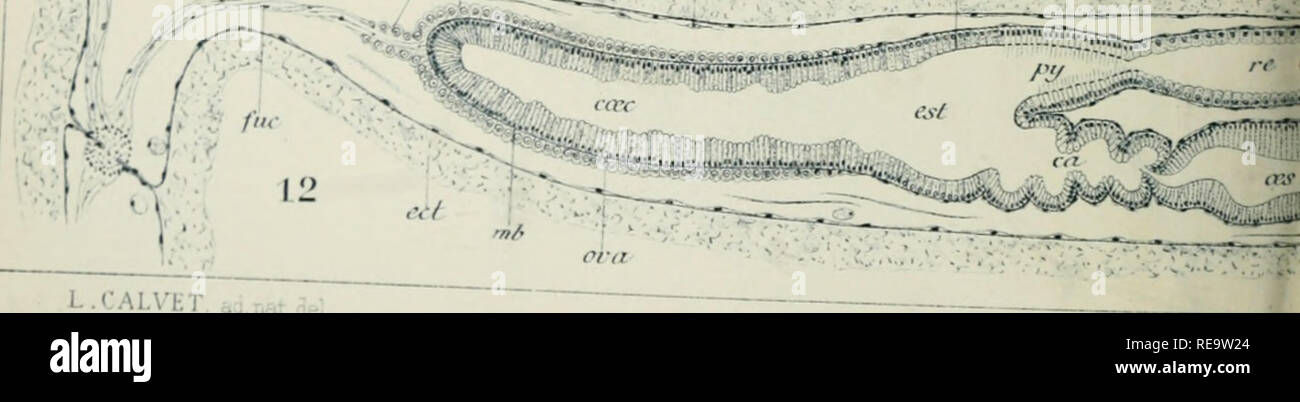
Contribution A L Histoire Naturelle Des Bryozoaires Ectoproctes Marins Bryozoaires Y P Quot A C R L N V A W F Eca C Lt Jlj T A A X A T A A L J L Calvet Natae Please

Typo A B C D E F G H I J K L M N O

Typo A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 3d Neon Fonts Modern Alphabet

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Galvanized Letter Other Home Decor Home Garden

Spelling Scheme Of Work Ppt Download

A B F G J M Q R T U X Gymnomitrion Parvitextum C E H I Download Scientific Diagram

Ceramic Abstracts 1963 Journal Of The American Ceramic Society Wiley Online Library

Typo A B C D E F G H I J K L M N O